Photorefraction
Ai-Hou Wang, M.D., Ph.D.
��v����k�O�άۤ��O�����դϥ��A�Ѭۤ��W�����ϥ����j�p�h���R�B�PŪ�����̪��}���ȡC�ثe���\�h�]�p�A�ϥΦP�˪����ǭ�z�A���άۤ��ӬO�ο��v�B�ιq���A�]����Ķ���u��v����k�v�C�ثe���⪺��v�����(photorefractor)���ĥ����b��v��������ǭ�z�C
Photorefractory
optics uses photographs to record pupil reflections and analyzes the magnitude
of the red-eye reflection in the photograph to determine the subject's
refractive value. Currently, many designs use the same optical principle but
instead of photographs, they use video recordings and computers; hence, they
are collectively translated as "photorefractory optics." Most
commercially available photorefractors currently
employ the optical principle of off-axis photorefractory optics.
��v����k���^��Ophotorefraction�Cphoto�����O�ۤ��A��N�O�άۤ��O�����դϥ��A�����ժ��ϥ�Ū�X���y���}���ȡA�ѭ^�媽Ķ�O�u�ۤ�����k�v�C�ثe���\�h�ϥΦP�˥��ǭ�z���]�p�A���O���άۤ��A�ӬO�ο��v�A�ιq���A�]����Ķ���u��v����k�v�ᬰ�A���C
The
English term for photographic refraction is "photorefraction."
"Photo" refers to a photograph, and the original meaning was to
record the reflection of light from the pupil using a photograph,
and then read the refractive value of the eye from the reflection. A
direct translation from English would be "photographic refraction."
Currently, many designs use the same optical principles, but instead of
photographs, they use video recordings and computers; therefore, the general
translation "photographic refraction" is quite appropriate.
��v����k�O�b�@�q�Z��
(50~100+cm)���~���, �ר�A�X���������C�b�@�q�Z�����~����@���O�p�����v���ڷQ�C�@�몺������Τ���������
(�ҦpNikon Retinomax)�B�Y�K�O�������˼v�k�]�o�ϥΤ��M����A���n�D�`���a������ժ̡C�Ӫ��նZ��������q�`�|�`�ȷ|���A�P�ɤ]�L�k�`��������}�̪������C
Photorefractive
refraction is performed at a distance (50-100+ cm), making it particularly
suitable for infants and young children. Performing refraction at a distance
has always been a dream for pediatric ophthalmologists. Regular or handheld
refractometers (such as the Nikon Retinomax), and
even retinoscopy, require the use of neutralizing lenses and must be very close
to the subject. Testing at such close distances usually frightens infants and
young children, causing them to cry, and they also cannot focus on the target
inside the refractometer's aperture.
��1
�`
��v����k���o�i
1.1 ��v��������o�i�v
1970�~�N�_�AHowland�MKaakinen����o�i�F�P�b (coaxial) �M���b (off-axis)����v����k�C�����M���Y�P�b����ؤ覡�O(1)������v��� (Orthogonal
photorefraction, 1974) �M(2)�U�V�P����v��� (Isotropic
photorefraction, 1979)�CKaakinen
1979�o�i�X���b��v��� (Eccentric photorefraction or
Knife edge photorefraction) (��4-1)�A�N�۾����{���O���챵�����Y�����A�q�ۤ��W�����ϥ����j�p�h���R�B�PŪ�����̪��}���ȡC�ثe���⪺��v����� (photorefractor)���ĥ����b��v��������ǭ�z�C
Section
1 Development of Photorefractory Methods
1.1
History of Photorefractor Development
Starting
in the 1970s, Howland and Kaakinen successively developed coaxial and off-axis
photorefractory methods. The two methods of coaxial light source and lens are
(1) orthogonal photorefractory (1974) and (2) isotropic photorefractory (1979).
Kaakinen developed off-axis photorefractory (Eccentric photorefractory or Knife
edge photorefractory) in 1979 (Figure 1), which involves moving the camera
flash closer to the center of the lens and analyzing and interpreting the
refractive value of the subject based on the magnitude of red-eye reflection in
the photograph. Currently, commercially available photorefractors
all use the optical principle of off-axis photorefractory.
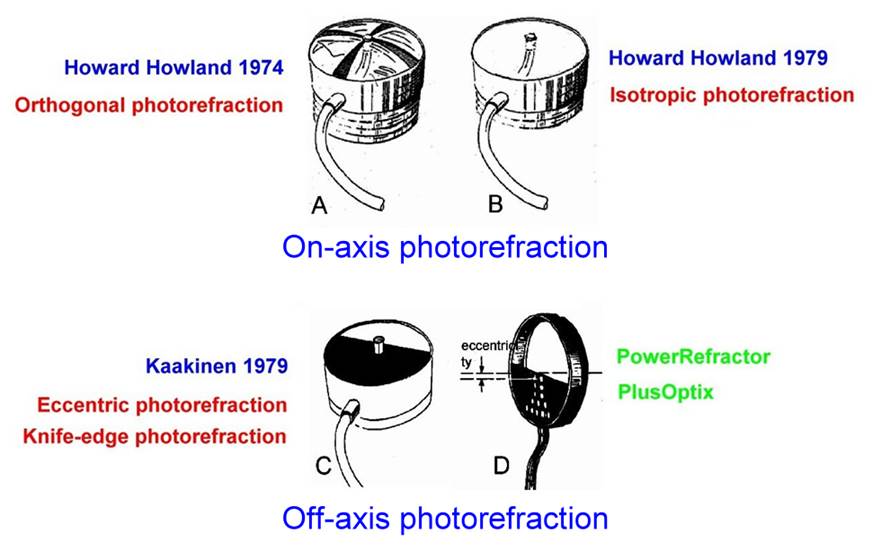
Figure 1 Orthogonal photorefraction,
Isotropic photorefraction,
and Eccentric photorefraction
1.2 ��v��������p
������v�������Plusoptix S12 (�e����PowerRefractor)�AWelch Allyn���q��SPOT (�e����Suresight)�A2Win�AiSreen�CGobiquity GoCheckKids�h�չϨϥ�iPhone�ӧ@��v����k�C��������v������h��MTI�AViVA�ATopcon���q��PR-1000�APR-2000�����C�o�ǻ����j���¦V���������V�]�p�A���O���q���ǽT�פ�DzΪ�������t�ܦh�A���A�X�@��T������t��A�ӬO�Ω�Τp�����E����z�Ϊ������B����Ҫ����O�z�ˡC�]���H��ij�b�H����ϳ]�m��v����F (booth)�A�n���֩�ۤ��F�@�ˡA�q���۰ʧPŪ�A�ݼs���O�z�˪��d��P�h���C
1.2 Market Status
of Photorefractive Optometrists
Commercially available photorefractive optometrists include Plusoptix S12 (formerly PowerRefractor), Welch Allyn's SPOT (formerly Suresight), 2Win, and iSreen. Gobiquity GoCheckKids attempts to use an iPhone for photorefractive
optometry. Early photorefractive optometrists included MTI, ViVA, and Topcon's PR-1000 and PR-2000. These
instruments are mostly designed
to resemble traditional refractometers, but their measurement accuracy is much lower,
making them unsuitable for precise refraction and prescription glasses. They
are better suited for
initial screening in ophthalmology or pediatric clinics, or vision
screening in kindergartens and daycare
centers. Some have proposed
setting up photorefractive optometry
booths in high-traffic
areas, similar to quick photo booths,
with automatic computer interpretation to broaden the
scope and level of vision screening.
�b�����W�A��v����k��Ƥ���ԲӪ����}�OABCD
(Alaske Blind Children
Discovery http://abcd-vision.org/ ���U��Vision
Sceening�A�A���U��Photoscreening http://abcd-vision.org/vision-screening/photoscreening.html�C
On the internet, the most detailed information on photorefraction
is available at ABCD (Alaske Blind Children Discovery
http://abcd-vision.org/, under Vision Sceening, and then Photoscreening
http://abcd-vision.org/vision-screening/photoscreening.html).
��2�` ��v����k������
��v����������άO�N��߱o�۾����{���O��U�A���m��D�`�a�����Y��������m (��4-2)�A�����դϥ�(Crescent)���j�p�ӧPŪ�ơC
Section
2 Optics of Photographic Optometry The prototype of the photographic optometry
instrument was to remove the flash of an instant camera and move it to a
position very close to the center of the lens (Figure 4-2), and to determine
the diopter by the size of the pupil reflection (Crescent).

��4-2
��߱o�۾���˰{���O�Ӧ�����v�����������
Figure
2 A prototype of a photographic optometry device made by modifying a Polaroid
camera into a flash unit.
�C�Ʃ}�������S�����դϥ��A���ת�������դϥ��b�{���O���P���A�Ӱ����������դϥ��b�{���O���t��
(��4-3)�C�b�C�Ʃ}�������A�Ҧp����+2D�M+3D�A�ϥ����j�p�t���ܤj�A��}����Ų�O�רΡF�Ӧb���Ʃ}�������A�Ҧp����+7D�M+8D�A�ϥ��j�p���t���N�ܦ����A�}����Ų�O�״N���n�F�C
Low-degree
refractive errors show no pupillary reflection. In high myopia, the pupillary
reflection is on the same side as the flash, while in high hyperopia, it is on
the opposite side (Figure 4-3). In low-degree refractive errors, such as
hyperopia +2D and +3D, the difference in reflection size is significant,
resulting in good refractive discrimination. However, in high-degree refractive
errors, such as hyperopia +7D and +8D, the difference in reflection size is
very limited, leading to poor refractive discrimination.
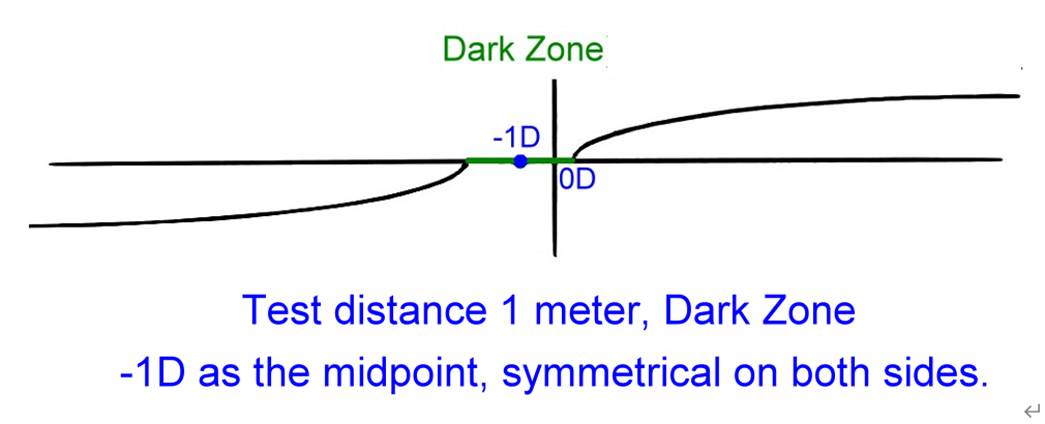
��4-3��b���}���ȡA�a�b���ϥ��j�p�C����B���������դϥ��b�ۤϰ��C
�ϧΪ���٤��I�O���նZ�����J��(vergence)�C
Figure
3 shows the refractive index on the horizontal axis and the reflectance on the
vertical axis. The pupillary reflectance is on opposite sides for myopia and
hyperopia.
The
midpoint of the graph represents the vergence at the test distance.
2.1 ��v����k�����Ǥ���
��v����k�����Ǥ����O�d�D���j��Howard
C. Howland (��4-4)�������X�A1999�~�ڦb�����������p�U�]�ۦ�ɥX�P�˪������C
2.1
Optical Formula of Photorefraction The optical formula of photorefraction was
first proposed by Howard C. Howland of Cornell University (Figure 4-4). In
1999, I also derived the same formula on my own without knowing the facts.

Figure 4 Dr. Howard
C. Howland
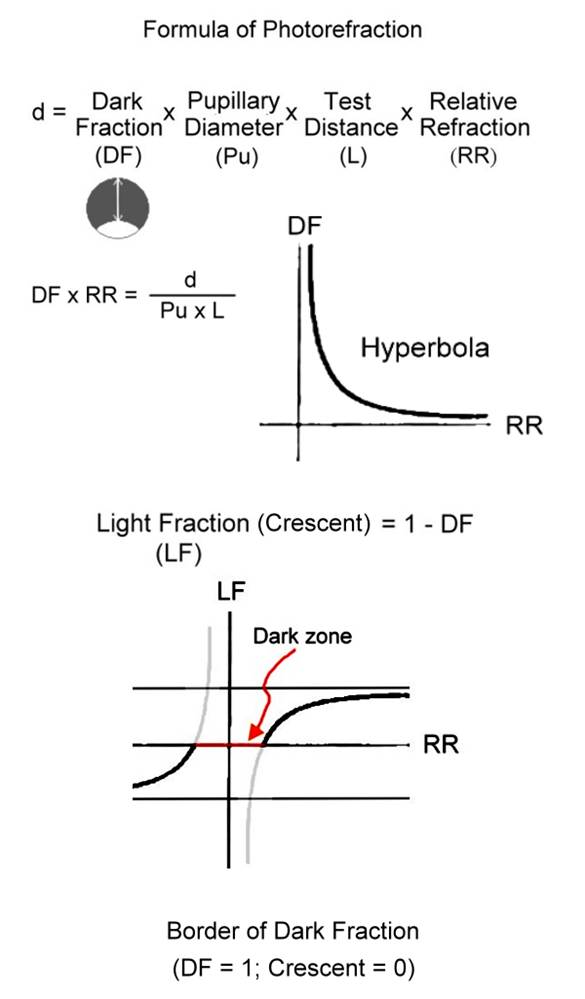
�����Ǥ����O d = DF x Pu x L x RR
* d�G���u�B���u���Z��(�Ϊ̬O�{���O��t�M���Y���ߪ��Z��)
* DF
(Dark Fraction)�G�t�Ϥ��
(=1�VCrescent) (1-�G�Ϥ��)
(��4-5)�A
�b�o�ӨҤl�̡A�t��=3/4�A�G��=1/4)
* Pu�G���ժ��|
* L�G���նZ��
* RR (Relative refraction)�G�۹�}���C�Ҧp�b1���ضZ���@���աA�h�H -1D������I�C- 4D��RR�O -3D�B��������RR�O +1D�B+3D��RR�O + 4 D�����C
The basic optical formula is d
= DF x Pu x L x RR
* d: Line of sight, distance of
light (or the distance between the edge of the flash and the center of the
lens)
* DF (Dark Fraction): Dark area
ratio (=1 �V Crescent) (1 �V Bright area ratio) (Figure 4-5). In this example,
dark area = 3/4, bright area = 1/4.
* Pu: Pupil diameter
* L: Test distance
* RR (Relative refraction):
Relative refraction. For example, when testing at a distance
of 1 meter, -1D is used as the reference point. -4D RR is -3D, RR for
emmetropia is +1D, RR for +3D is +4D, and so on.
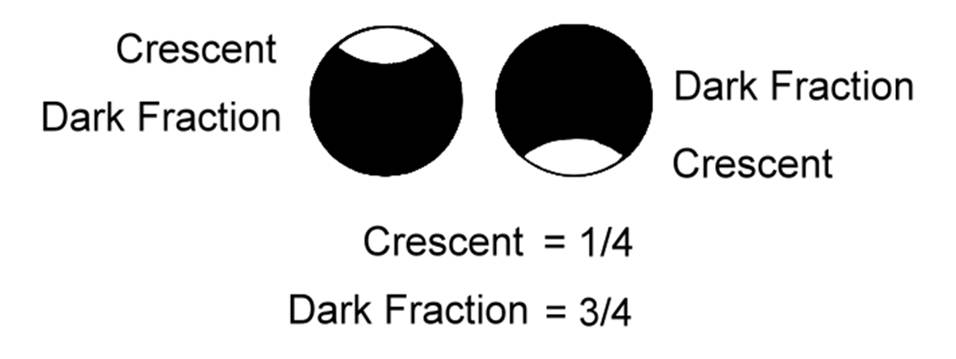
��4-5
�t�ϡB�G���P���ժ���ҡC�����ϥܫG��/����=1/4�A�t��/����=3/4�C
Figure
5 shows the ratio of dark area, bright area, and pupil. In this example, the
ratio of bright area to pupil is 1/4, and the ratio of dark area to pupil is
3/4.
�צV���������դϥ�
(Crescent)�]�O�ɱת� (��4-6)�C�չϪ����q�צV�ϥ����Ϊ��B���ץh�p��}���������аѦ�Wesemann
W, Norcia AM, Allen D. Theory of eccentric photorefraction (photoretinoscopy):
astigmatic eyes. J Opt Soc Am A. Dec;8(12):2038-47,
1991.
The
pupillary reflection (Crescent) in oblique astigmatism is also oblique (Figure
4-6). For formulas that attempt to calculate refractive error directly from the
shape and angle of the oblique reflection, please refer to Wesemann W, Norcia
AM, Allen D. Theory of eccentric photorefraction (photoretinoscopy):
astigmatic eyes. J Opt Soc Am A. Dec;8(12):2038-47,
1991.

��4-6
�צV���������դϥ��]�O�ɱת�
Figure
4-6 shows that the pupillary reflection in oblique astigmatism is also oblique.
2.2 PowerRefractor
PowerRefractor�ѤT�Ӥ�V�������AŪ���T�Ӥ�V���ƾڥh�@��v����k
(��4-7)�C�o�T����V�����ܤ֦���Ӥ�V�����դϥ��O�ɱת��ϥ��A�]���w�O�Q�θӽg�פ媺�p��覡�h�D���}���ȡC�@�몺�}���ȥ]�t���y����B�W����M�W�����פT���ܼơAPowerRefractor���q�T�Ӥ�V���ƭȥh�ഫ���}���Ȫ��T���ܼơA�]��O���X�z���C
2.2 PowerRefractor The PowerRefractor uses light from three directions to read
data from each direction for photorefraction (Figure 4-7). At least two of
these directions show oblique pupillary reflections, and the refractive value
is calculated using the method described in this paper. A typical refractive
value includes three variables: spherical power, cylindrical power, and
cylindrical angle. It is reasonable for the PowerRefractor
to measure values from three directions and convert them into these three
variables for the refractive value.

��4-7 PowerRefractor���q�T�Ӥ�V���ƾڥh�p�Ⲵ�y�}���Ȫ��T�ܼơG
(1)�y����B(2)�W����B(3)�W�訤���C
Figure
4-7 PowerRefractor measures data in three directions
to calculate the three variables of the eye's refractive value: (1) spherical
power, (2) cylindrical power, and (3) cylindrical angle.
2.3 ���������誺���ǵ��c
���������誺���ǵ��c�����ŦX��v����k�����ǭ�z�A���F����g�ѷ��p�����եh�ˬd�����A���������M���u�]�p���D�`���a��
(��4-8)�A�X�G�O�P�b���C
2.3
Optical Structure of Direct Fundus Camera The optical structure of the direct
fundus camera fully conforms to the optical principles of photorefraction. In order to examine the fundus through the extremely small
pupil, its light source and line of sight are designed to be very close (Figure
4-8), almost coaxial.
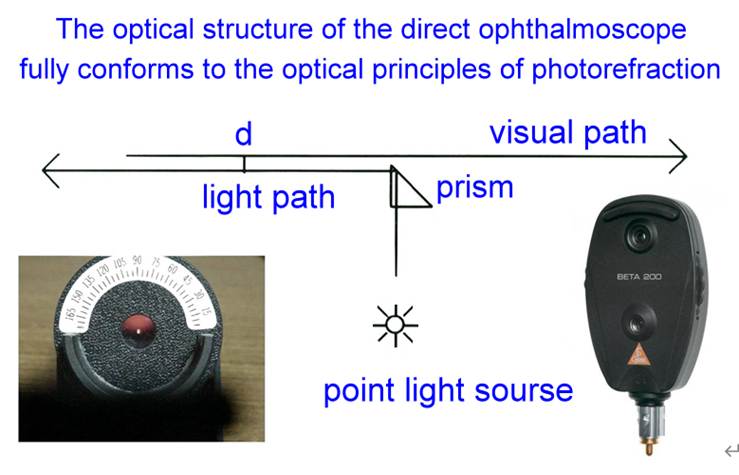
��4-8
���������誺���ǵ��c�����ŦX��v����k�����ǭ�z
Figure
4-8 shows that the optical structure of the direct fundus microscope fully
conforms to the optical principles of photorefraction.
�q50~
From a
distance of 50-100 meters, observe the patient's pupillary red reflex
through the viewing port of a direct ophthalmoscope (similar
to the Hirschberg test for strabismus). Low-degree refractive errors
fall within the non-reflective zone of photorefraction, resulting in no
pupillary reflex and a dark pupil. If a reflex (crescent) is seen above the
pupil, it indicates high hyperopia; if a reflex is seen below the pupil, it
indicates high myopia (Figure 4-9). This is very useful in pediatric
ophthalmology examinations, allowing for a preliminary assessment of the
approximate refractive state without the need for a neutralizing lens.
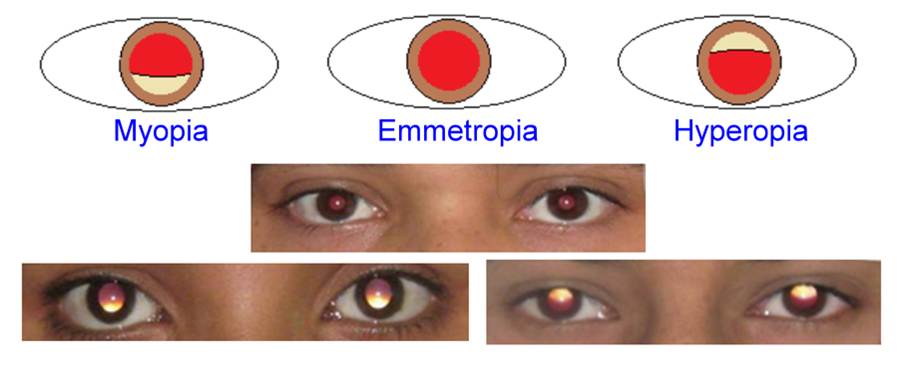
�� 4-9 �Ѫ��������誺���լ����դϥ��A���դU�観�ϥ� �i�P���O����
������A���դW�観�ϥ��O���������C
Figure 4-9 shows the pupil reflection as seen through the viewing aperture of a
direct ophthalmoscope. A reflection below the pupil indicates high myopia,
while a reflection above the pupil indicates high hyperopia.
2.4 Brückner�ϥ��ˬd
���ժ�Brückner�ϥ��ˬd�����ǭ�z�]�p�P��v����k�@�ˡC�b�@�q�Z���B�Ѫ��������������զP���ݨⲴ�����դϥ��A���շt���@���O�`�����A�åB�O�C�Ʃ}�������F���իG���@���O�����A�]���O�ѱת���V�[��o�Ӳ����A���ǤW�O�������A��O���զ��ϥ��A�O�G������ (��4-10)�C
2.4
Brückner Reflection Test
The
optical principle of the Brückner reflection test of the pupil is the same as
that of photorefraction. At a distance, the pupil reflections of both eyes are
simultaneously observed through the viewing aperture of a direct
ophthalmoscope. The eye with a darker pupil is the fixing eye and has a low
degree of refractive error; the eye with a brighter pupil is the strabismic
eye, because it is being observed from an oblique direction, optically it is
highly hyperopic, hence the bright pupil (Figure 4-10).
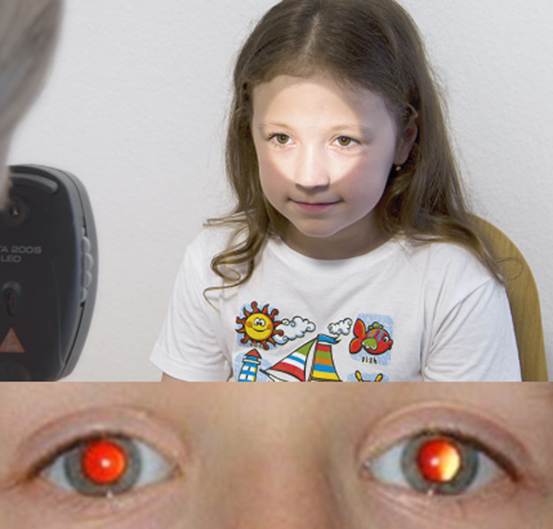
��4-10 Brückner���դϥ��ˬd�C���իG���@���O�����C
Figure
4-10 Brückner pupillary reflection test. The eye with the brighter pupil is the
strabismic eye.
2.5 �@����v���������D
�@�몺�۾���H�����ɭԡA���Ʊ������յo�G�A��O�{���O����m���q���n�Ӿa�����Y�H�K���ͬ����C���O��v����k�N�O�n�Q�γo�Ӥϥ��h�PŪ���y���}�����A�A�]���S�a�N���u�M���u�a�o�ܪ�A�p�P���������誺�c�y���ˡC
2.5 Red-eye in General Photography When shooting portraits with
a regular camera, it's best to avoid capturing bright pupils, so the flash is
kept as close to the lens as possible to prevent red-eye. However, photographic
refraction uses this reflection to determine the refractive state of the eye,
so the light source and line of sight are deliberately brought very close, similar to the structure of a direct ophthalmoscope.
2.6 �H���������誺�����@�������������ˬd�������ϥ�
������������ǭ�z�]�O�@�ˡA���u�M���u���q�a��~�ݱo�체���A���u�����u�ӻ��N�ݤ��체���F�C���������誺�I�����A�i�H�@�������������ˬd�������ϥΡA�]�����ե����i�վ�G�סA�S�O�A�X�p��쪺�����ˬd (��4-11)�C�q�����誺���լ��X�h�A�����������ˬd�ҥΪ��Y�z��|�ϥ��A�]���q�`���O�����դ��~����m�h�[��C�p�G�����M���u���Z�� (d) �Ӥj�A�Ѥ����i���A�b�C�Ʃ}���������t�Ϸ|�ܼe�A���Q�����������ˬd�����C�N��������������W�t����ؾ��q���p�A���ǤW�N�i�H��ŦX�����������ˬd�������n�D�C
2.6
Using the Light Source of a Direct Ophthalmoscope as a Light Source for
Indirect Ophthalmoscopy
The
optical principle of indirect ophthalmoscopy is the same: the fundus can only
be seen when the light source and the line of sight are as close as possible;
if the light source is too far from the line of sight, the fundus
cannot be seen. The point light source of a direct ophthalmoscope can be used
as a light source for indirect ophthalmoscopy because it has a dimmer to adjust
the brightness, making it particularly suitable for fundus examinations in
pediatric ophthalmology (Figure 4-11). Looking out from the viewing aperture of
the ophthalmoscope, the convex lens used in indirect ophthalmoscopy will
reflect light; therefore, observation is usually performed from a position
outside the viewing aperture. If the distance (d) between the light source and the
line of sight is too large, as shown by the formula, the dark area in low-power
refractive errors will be very wide, which is not conducive to indirect
ophthalmoscopy examination of the fundus. Making the
upper edge of the viewing aperture of the direct ophthalmoscope as small as
possible will better meet the optical requirements for the light source of
indirect ophthalmoscopy.
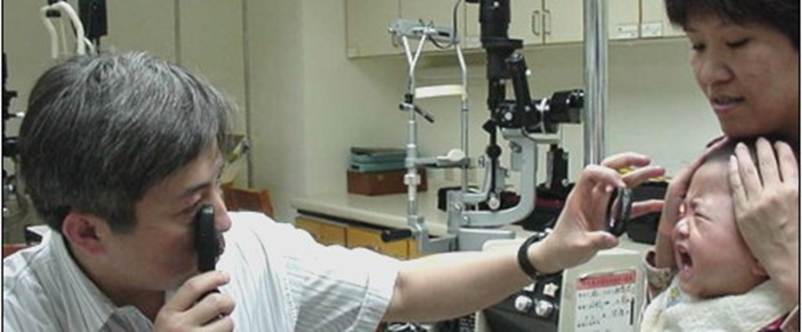
�� 4-11 �H���������誺�����@�������������ˬd�������ϥ�
Figure 4-11 shows the use of a direct ophthalmoscope
light source as a light source for indirect ophthalmoscopy.
��3
�`
�������v�����
d = DF x Pu x L x RR�����̡ADF(�t��)�MRR��b�������P���A�G�̬O�����u�����Y (��4-12)�C�ܩ�ϥ����G��Crescent����1-
DF�A��O�G�ϩM�}�������Y�K�p�U�ϩҥܡC��������v�����MTI�̤ϥ��G�Ϫ��j�p�h�PŪ�ơA��Crescent�M�}�������Y�ϨӬݡA�i�H���D�b�C�Ʃ}���d��A�HCrescent���j�p�h�PŪ�}�����ѪR���ΡF�b���Ʃ}���d��A�ѪR�״N�ܮt�C
Section
3 Handheld Photorefractive Optometry (MTI)
In the formula d = DF x Pu x L x RR, DF (dark area) and RR are
on the same side of the equation, and their relationship is hyperbolic (Figure
4-12). The reflected bright area (Crescent) is equal to 1 - DF, thus the
relationship between the bright area and refractive power is shown in the
figure below. Early photorefractive optometry (MTI) used the size of the
reflected bright area to determine the power. From the relationship between
Crescent and refractive power, it can be seen that in
the low refractive power range, using the size of Crescent to determine the
refractive power resolution is better; in the high refractive power range, the
resolution is very poor.
��4-12 DF(�t��)�MRR(�}��)��b�������P���A�G�̬O�����u�����Y�C
�G��(=1-�t��)�MRR(�}��)�����u�O��2-30���ƾǭp��C
In
Figure 4-12, DF (dark area) and RR (refractive error) are on the same side of
the equal sign, and their relationship is hyperbolic.
The
curves for the bright area (=1-dark area) and RR (refractive error) are
mathematical calculations based on Figure 2-30.
d = DF x Pu x L x RR�����̡Ad�MRR�O��b�������ⰼ�A��̬O�u�����Y�C�L�צb����}���d��A�Hd�PŪ�}�������P�˦n���ѪR�סCHoward�̦������b��q���e����m�@������˪��ȪO
(��4-13)�A�q���誺��t�[�����դϥ��A���۶��誺�Ʀr�v��V�W�A���u�B���u���Z�������Ի��A�ϥ�Crescent�V�ӶV�p�A��F���誺�Y�@��ɤϥ������A�o��Crescent=0�ADF=1�A�̾ڤ����ARR
= d / Pu / L�A�p�G���D���դj�p(Pu)�M���նZ��(L)�A�N�i�H��d���Ǧa���X�}����(RR)�F�C
In the formula d = DF x Pu x L x RR, d and RR are on opposite
sides of the equals sign, and they have a linear relationship. Regardless of
the refractive range, interpreting refractive errors using d provides equally
good resolution. Based on this concept, Howard placed a stepped cardboard plate
in front of a flashlight (Figure 4-13), observing the pupillary reflection from
the edge of the plate. As he moved upwards along the numbered steps, the
distance between the line of sight and the light gradually increased, and the
reflection (Crescent) decreased. At a certain step, the reflection disappeared,
at which point Crescent = 0 and DF = 1. According to the formula RR = d / Pu /
L, if the pupil size (Pu) and the testing distance (L) are known, the refractive
value (RR) can be accurately calculated from d.

��4-13
��q���e����m�@������˪��ȪO�A���u�B���u���Z�������Ի��A�ϥ�Crescent�V�ӶV�p�C
�ϥ������B�ACrescent=0�ADF=1�A�̾ڤ����ARR
= d / Pu / L�C
Figure
4-13 shows a stepped cardboard panel placed in front of a flashlight. As the
distance between the line of sight and the light source gradually increases,
the glare (Crescent) decreases.
At the
point where the glare disappears, Crescent = 0, DF = 1. According to the
formula, RR = d / Pu / L.
�q�o�˪����ΡA�ڭ̺c��í�ij�F�������v��������s�@�C
From
this prototype, we conceived and advocated for the development of a handheld
photorefractive refractometer.
���e���g�N�o�ӷ����ФѬz���Ǽt�}�һs�@�A�]�M�x�j��|��u���X�@�A��yHeine��������A�s�@�L��B�����~
(��4-14)�C���ժ̤W�U���ʱ���A���ܵ��u�B���u���Z���A�ѵ����[�����դϥ����j�p�A �ϥ����j���p�A�H�ϥ������I (DF=100%=1)�@���PŪ���̾ڡAŪ�X�}���ȡC
Previously,
we commissioned Tianjin Optical Factory to develop and manufacture molds for
this concept. We also collaborated with the Biomedical Engineering Department
of National Taiwan University Hospital to modify Heine's fundus lens and
produced a preliminary finished product (Figure 4-14). The tester pushes the
lever up and down to adjust the distance between the line of sight and the
light source, and observes the size of the pupil
reflection through the viewing port. The reflection gradually decreases, and
the vanishing point of the reflection (DF=100%=1) is used as the basis for
interpretation to read the refractive value.

��4-14
a�Ѭz���Ǽt�s�@�������v���������
Figure
4-14 a Prototype of a handheld photorefractive optician manufactured by Tianjin
Optical Factory
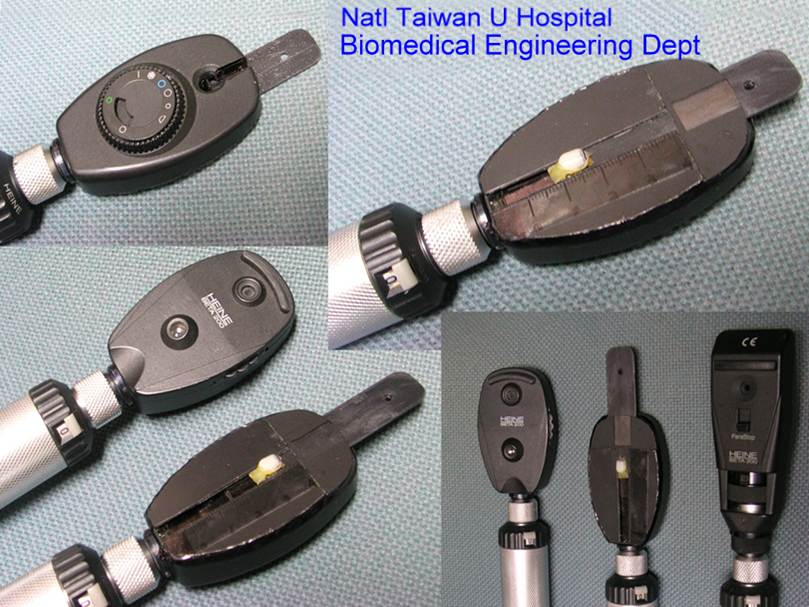
��4-14
b�x�j��|��u���s�@�������v���������
Figure
4-14b shows a prototype of a handheld photorefractive refractometer produced by
the Biomedical Engineering Laboratory of National Taiwan University Hospital.
�Ҧp����������
For example, if the pupil is 8mm after
dilation and the test distance is 0.5m, applying the formula d = DF x Pu x L x RR, we get d = 1 x 8 x 0.5 x RR �� d =
4mm x RR. This means that
in any refractive range, 1D
refractive power has a resolution
of 4mm, which should be very practical.
�M���⪺��v��������P���O�A�L�̴¦V���������V�]�p�A�ӧڭ̭�ij�²�����/�����誺��V�h�]�p�B�h�s�@�@�����������v������C����b������E�`�W�]�m������������M�����褧�~�A�A�K�@��p������Ϊ��Q���C
Unlike
commercially available photorefractive instruments,
which are designed like refractometers, we advocate designing and manufacturing
a handheld photorefractive instrument that resembles a
fundus microscope/retinal microscope. Our hope is to add another useful tool
for pediatric refraction, in addition to the direct fundus microscope and
retinal microscope routinely provided in ophthalmology clinics.
�p�e�ҭz�A�������������v������O�ѱצV�����դϥ��h�p��}���ȡA�ӧڭ̭�ij���������v������O�Ѵ��ժ̱N�����վ�ܴ����b����V (��4-15)�A����ѥ��V�����դϥ��PŪ�}���ȡA������������˼v�k�PŪ�������ת��@�k�C�ڭ̷Pı�ѥ��V�����դϥ��h�PŪ�}�������ӷ|��[�����M�ǽT�C
As
mentioned earlier, refractometer-type radiographs calculate refractive values
based on oblique pupillary reflections. However, our proposed handheld
radiograph method involves the user adjusting the light source to align with
the astigmatic axis (Figure 4-15), and then
interpreting the refractive value using positive pupillary reflections, similar to how retinoscopy is used to determine the
astigmatic angle. We believe that interpreting refractive power using positive
pupillary reflections would be more direct and accurate.
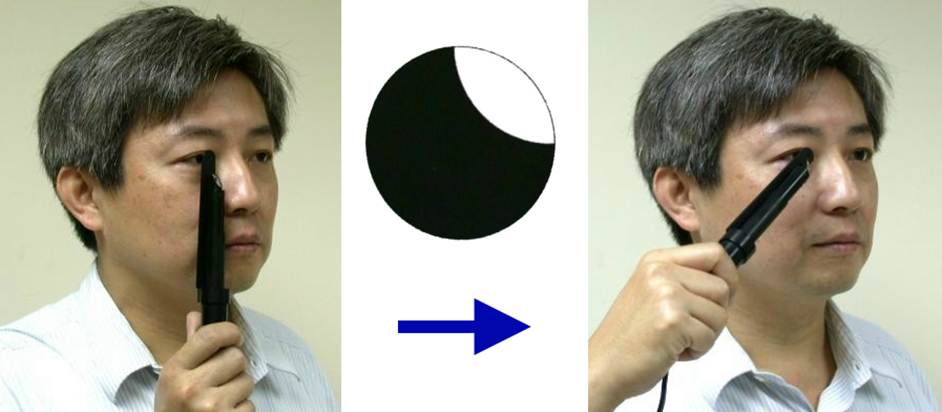
��4-15
�������v������O�Ѵ��ժ̱N�����վ�ܴ����b����V
Figure
4-15 shows a handheld photorefractive refractometer, in which the tester
adjusts the light source to the direction of the astigmatic axis.
�������v����k�����[�����դϥ�����V�A���ܴ��������סF������ܤϥ����j�p�A�hŪ���o�Ӷb�V���}���ȡA�A��90�סA���ܤϥ��j�p�AŪ���t�@�Ӷb�V���}���ȡC �D�`������������˼v���ާ@��k�A���O���ݭn��m���M����A�a����������e�A�i�H�קK������`�ȡB�k�שM���x�C
The handheld photorefractive method first
observes the direction of the pupillary reflection and adjusts the angle
of astigmatism; then it
adjusts the magnitude of the reflection
to read the refractive
value along this axis, then rotates 90 degrees, adjusts the magnitude of
the reflection again, and reads the refractive value along the other axis. It is very similar
to the procedure for retinal
retinoscopy, but it does not require the placement of
a neutralizing lens. It is placed close to the infant's eyes, which can prevent the infant from becoming afraid,
trying to escape, or crying.
���⪺��v������n�b�T�w���Z���@���աA�վ���ժ��Z���`�`�ݭn��ɶ��h�˷ǵ����C�{������ަ��D�`��T�����Z���A�p�G�i�H���ش��Z���A�����o�줽���̪�L�A�N�����b�T�w���Z�����աA�ӥB�}����R=RR-1/L�]�i�H��L�Ȼ��P�p��o��C
Commercially available refractometers require testing at a fixed distance, and adjusting the
testing distance often takes time to aim at the target. Modern technology offers highly accurate
rangefinders. If a rangefinder
could be built-in to directly obtain the value of L in the formula, testing
at a fixed distance would be unnecessary, and the refractive value R = RR - 1/L could
be easily calculated from the value of L.
���������ժ����|Pu�A�L�״����P�_�A�]�i�H�Q�ιq���ϾǪ�����q�o���C���@�������v���������ij�ݱo�̿��u��|���ѻP�B�]�p�P�I�Ѱ���C
The pupil diameter
Pu in the formula can be measured
using computer graphics technology, regardless of whether the pupil is dilated. This proposal for a handheld photorefractive refractometer requires the participation, design, and implementation
of the Industrial Technology
Research Institute (ITRI).
Recommended
readings and references
1. Howland
HC, Howland B. Photorefraction: a technique for study of refractive state at a distance. J Opt Soc Am 1974;64:240-9.
2. Howland HC, Braddick O,
Atkinson J, Howland B. Optics of photorefraction: orthogonal and isotropic
methods. J Opt Soc Am 1983;73:1701-8.
3. Howland HC. Photorefraction of eyes: history and future
prospects. Optom Vis Sci 2009;86(6):603-6.
4. Howland HC, Sayles N,
Cacciotti C, Howland M. Simple pointspread
retinoscope suitable for vision screening. Am J Optom Physiol Opt 1987;64(2):114-22.
5. Kaakinen K. A simple method
for screening of children with strabismus,
anisometropia or ametropia by simultaneous photography of the corneal and
fundus reflexes. Acta
Ophthalmol 1979;57:161-71.
6. Kaakinen K. Photographic
screening for strabismus and high refractive errors of children aged 1�V4 years.
Acta Ophthalmol (Copenh) 1981;59:38�V44.
7. Wang AH. Photorefraction and
retinoscopy with direct ophthalmoscope and laser pointer. Invest Ophthalmol
Vis Sci 1999:30(4):56.
8. Wang AH. Handheld photorefractor. 18th Congress of the Asia-Pacific
Academy of Ophthalmology, March 10-14. 2001, Taipei, Taiwan.
9. Wesemann W, Norcia AM, Allen
D. Theory of eccentric photorefraction (photoretinoscopy):
astigmatic eyes. J
Opt Soc Am (A) 1991;8:2038�V47.
This
article is dedicated to the teachers at The Smith-Kettlewell Eye Research
Institute (SKERI): Dr. Arthur Jampolsky, Dr. Alan Scott, Dr. Anthony Norcia,
Dr. Eric Sutter, and Dr. Christopher Tyler. I vividly remember my year as a
pediatric ophthalmology fellowship in San Francisco, a place brimming with
talent and beauty, from 1990 to 1991.
Author:
Ai-Hou Wang

Education:
Bachelor of Medicine, National Taiwan University / Doctor of Clinical Medicine,
National Taiwan University / Fellow, Pediatric Ophthalmology and Strabismus,
The Smith-Kettlewell Eye Research Institute (SKERI) and Pacific Presbyterian
Medical Center, San Francisco, USA.
Experience:
Resident and Attending doctor, Ophthalmology Department, National Taiwan
University Hospital / Associated Professor, Ophthalmology Department, National
Taiwan University College of Medicine.
Current
Position: Consultant, Ophthalmology Department, Cathay
General Hospital / Attending doctor, Universal Eye Center.