設計心理物理學實驗 – 強迫選擇和階梯式趨近閾值

Designing Psychophysical Experiment – Forced choice and Staircase approach

王藹侯

強迫選擇 (Forced choice)

強迫選擇法最淺顯的說法就是你想要知道某件事，例如想要知道受試者是不是能看得到C或E視標的缺口，你要問另個題目 – 缺口的方向，答對缺口的方向，表示他看得到缺口。而不是直接問受試者“看得見缺口嗎？”，他回答“看得見”，換小一級的缺口，再問“看得見缺口嗎？”，他回答“看不見”。這樣測試，測試者和受試者都無法確實判別是不是真的可以看見那缺口。

Snellen E視力表的缺口有上下左右四個方向(見圖)，是4選項的強迫選擇(4-alternative forced choice, 4-afc)，也就是靠猜答對的機率是1/4，連續答對兩題，靠猜答對的機率更低，是1/16。

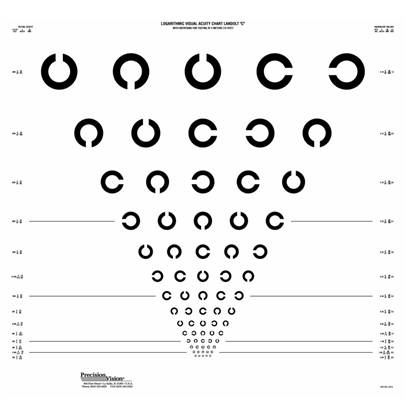
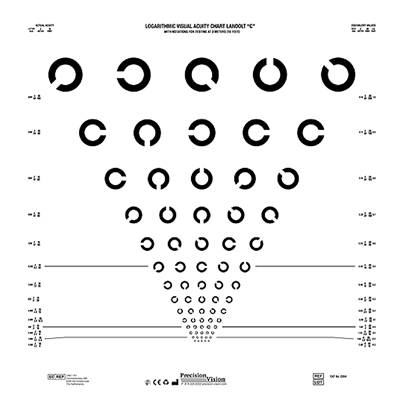
Landolt C視力表的缺口有上下左右4選項(4-afc)和加上斜右上、斜左上、斜右下、斜左下8選項(8-afc)強迫選擇兩種(見圖)。

我做小兒眼科的臨床經驗，大約兩歲半到三歲之間的小朋友可以學會指出C或E的缺口，但是斜向缺口的C常常造成困擾，不容易學習。

我們覺得8個缺口方向的C視力表徒增困擾、沒甚麼意義：使用上下左右4個方向的C視力表靠猜答對的機率是1/4，測兩次靠猜答對的機率是1/16，已經好過8個方向C視力表靠猜答對的1/8。

另外如果利用電腦螢幕做視力檢查，因為電腦螢幕的像點(pixel)是橫直方向排列的，斜向缺口的C視標程式設計上會有精準度的困難。

NTU300秒角亂點立體圖的設計也採用4選項的強迫選擇(見圖)。受試者可以答出隱藏的形狀，當作他有亂點立體視的指標。每次的測試靠猜答對的機率是1/4，林隆光醫師訂定篩檢過關的標準是連續答對5題，這樣靠猜答對的機率就只有(1/4)⁵=1/1024

這張對比敏感度(contrast sensitivity)檢查表是3選項(3-afc)的強迫選擇(見圖)，受試者回答線條是正的、左傾的或右傾的。

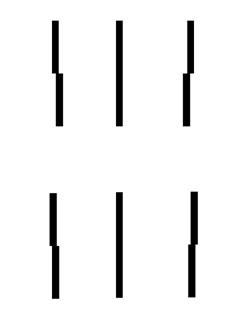
這張游標超視力(vernier hyperacuity, nonius lines)檢查表也是3選項(3-afc)的強迫選擇(見圖)，受試者回答上面的線段是在下面線段的正上、偏左或偏右。

階梯式趨近閾值 (Staircase approach)

以測視力(visual acuity)為例子，強迫選擇法知道了你看得到對數視力表0.4的缺口之後，再來就是要測對數視力表0.3的缺口是否看得見，0.2、0.1…去趨近、得到受試者的視力閾值，像我們一般在門診測試視力同樣的做法。

使用電腦自動化趨近閾值最常使用的是階梯式趨近閾值(見圖) – 這個例子是連續答對2題則題目變困難一階(向上一格)，答錯1題則題目變簡單一階(向下一格)，依據這個規則連續測試，得到如圖的摺線，折線來到第5個反轉點的時候測試結束，將5個反轉點的視力值取平均值，得到這次視力檢查的視力估計值。

由以上的陳述，我們知道設計一個階梯式趨近閾值的測試要事先決定的參數有：

1. 測試啟始處題目的難易度

2. 答對幾次題目變難

3. 答錯幾次題目變簡單

4. 幾次反轉結束測試

再一個例子如下：連續答對3題則題目變困難一階(向上一格)，答錯2題則題目變簡單一階(向下一格)，連續測試來到第6個反轉點的時候結束測試。

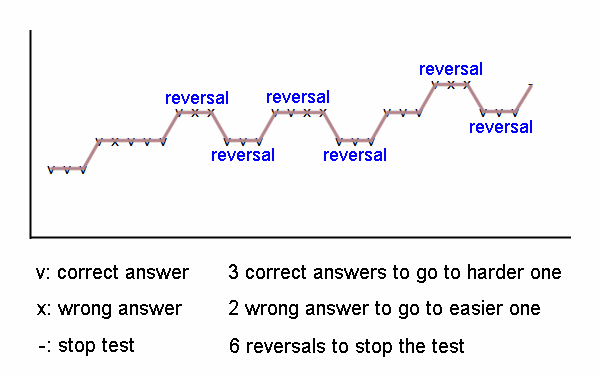
典型的測試視力的例子：

以對數視力0.4(Snellen 0.4)為起點

答對2次題目變難

答錯1次題目變簡單

5次反轉結束測試 (見圖)

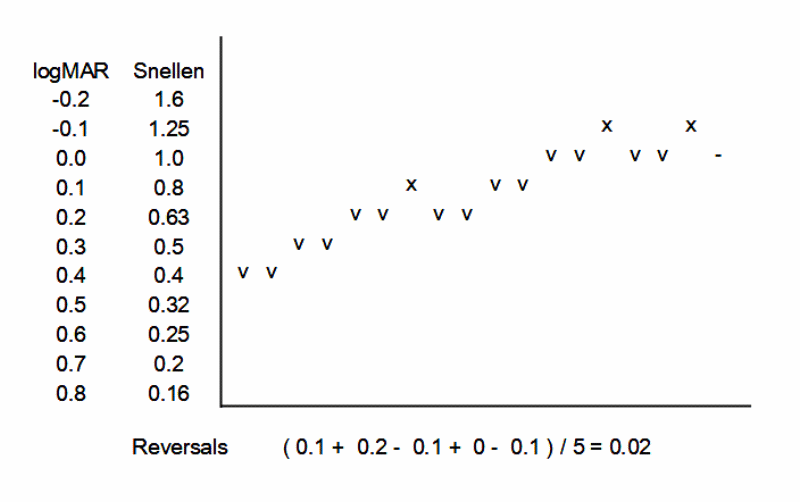
5個反轉點的對數視力值為0.1、0.2、-0.1、0和-0.1，平均值為0.02。

亦即視力估計值為對數視力0.02，相當於Snellen視力0.95。

這張是理想狀態的階梯式趨近閾值，受試者非常穩定 – 三個反轉高點都在Snellen 0.8，兩個反轉低點都在Snellen 0.63。

5個反轉點的對數視力值為0.1、0.2、0.1、0.2和0.1，平均值為0.14。

亦即視力估計值為對數視力0.14，相當於Snellen視力0.72。

設計階梯式趨近閾值的測試或實驗還有一點要注意，就是縱軸的刻度單位在心理物理學的基礎上必須是線性的(linear scale)，反轉點的算術平均數才好當作閾值的估計值。

目前一般的共識是以視角的對數做為單位的對數視力表每一行之間(視力進步一行或退步一行)是等距的，以之作為階梯式趨近閾值的縱軸單位是線性的。將反轉處的對數視力值做算術平均數，當作該次測試的視力估計值是合理的。

階梯式趨近閾值法最快速，也是最常用的參數就是如前所述的2上1下(答對2次題目變難、答錯1次題目變簡單)，但是在測試過程中以操縱桿(joystick)或鍵盤輸入答案時難免產生誤擊，在測試流程中於是產生了錯誤的反轉點(reversal)，造成錯誤的估計，則是要特別注意的。程式設計時要設計有發現錯誤輸入、修正錯誤輸入的方法，以減少錯誤的結果。

弱視的治療和視力測試也可以利用階梯式趨近閾值法同時解決：比方使用5上2下(答對5次題目變難、答錯2次題目變簡單)6反轉結束的策略，延長測試的時間，讓小朋友在將看得見、將看不見的情境下打魔鬼、採花蜜...，掙扎良久，達到治療弱視的目的，最終也得到他的視力值。在重複的弱視訓練中看他的視力慢慢進步。

這樣設計以電腦測試視力 – 每一步驟以強迫選擇法判定通過、不通過，接續的步驟則以階梯式趨近法去得到視力的閾值，受試者可以自行測試自己的視力，不需要依靠測試者幫你測試。

不只視力測試，測試任何視覺現象，像對比敏感度、游標超視力(vernier hyperacuity)、運動覺…的閾值，都可以用(強迫選擇＋階梯式趨近法)去得到。更廣泛的講，不只眼科，也不只臨床科系，所有心理物理的實驗，你想要知道對某一物理刺激的知覺反映的閾值，都可以利用同樣的方式去完成。

我以前在ARVO會議上就見識過PhD博士論文的內容，是博士生在電腦上以(強迫選擇＋階梯式趨近法)的方式設計實驗，受試者就博士生和指導教授兩人，就完成一篇論文！

如果你要探討的視覺內容很有價值，實驗設計夠嚴謹，受試者的測試資料夠穩定，其實這也無可厚非。